Java Program for Tower of Hanoi Problem

By Manish Fartiyal | Last Updated: January 19, 2020 Previous       Next

In this article, we are going to solve the Tower of Hanoi problem using Java program. There are two approaches to solve this problem one is the iterative approach and the second is the recursive approach.

In this, we will solve the Towe of Hanoi problem using the recursive approach.

Problem Statement

We are having three pegs and N number of disks. Now we must move all the disks from source peg to destination peg using an auxiliary peg. While performing operation we must keep in mind below conditions:

1. Larger radius disk can’t be placed on a smaller radius disk.
2. Move one disk at a time from one peg to another peg.

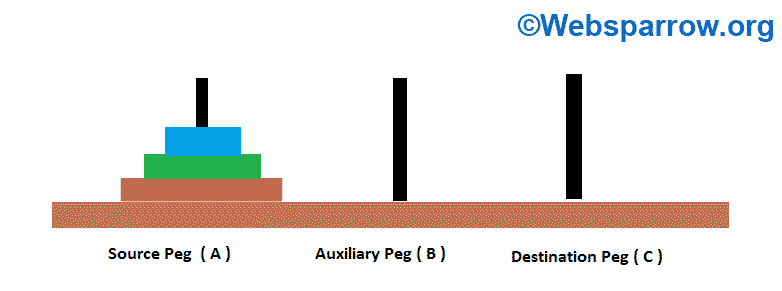
Initially, all disks are placed in ascending order.

Solution

The formula for calculating moves for solving N disks of Hanoi tower is:

Total moves = 2^N - 1

Here N is the total number of disks.

Steps to solve N number of disks via recursion:

1. First, move top N-1 disks to auxiliary peg.
2. Move N^th disk from source peg to destination peg.
3. Move N-1 disks form auxiliary peg to the destination peg.

Minimum moves to solve the Tower of Hanoi puzzle with 3 disks are as follows:

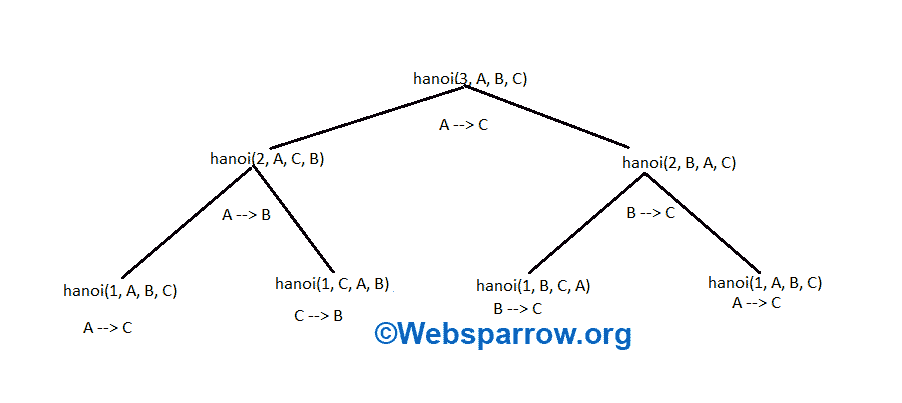
Move Form A –> C

Move Form A –> B

Move Form C –> B

Move Form A –> C

Move Form B –> A

Move Form B –> C

Move Form A –> C

Java Program

package org.websparrow;

public class TowerOfHanoi {

	public static void main(String[] args) {
		int n = 3; // number of disks
		hanoi(n, "A", "B", "C");
	}

	public static void hanoi(int n, String source, String aux,
			String destination) {
		if (n == 1) { // terminal state

			System.out.println("Move Form " + source + " --> " + destination);

			return;
		}
		hanoi(n - 1, source, destination, aux);

		System.out.println("Move Form " + source + " --> " + destination);

		hanoi(n - 1, aux, source, destination);
	}
}

Output

Move Form A --> C
Move Form A --> B
Move Form C --> B
Move Form A --> C
Move Form B --> A
Move Form B --> C
Move Form A --> C

References

1. Tower of Hanoi – Wikipedia
2. Tower of Hanoi – Wolfram MathWorld